Адаптивная итерация Эксп-Халлея с экспоненциальным корнем для надежного поиска корня в условиях шума

Аннотация

Мы представляем модификацию метода Халлея для решения уравнений $f (x) = 0$ , которая сочетает кубическую сходимость с адаптивным регуляризатором и экспоненциально-корневым базисом.
Метод сохраняет порядок сходимости Халлея в идеальных условиях и демонстрирует повышенную устойчивость при наличии вычислительного шума.

1. Введение

Классические итерационные методы — Ньютон ( $a_{k + 1} = a_{k} - f (a_{k}) / f^{'} (a_{k})$ ) и Халлей — обладают высокой скоростью сходимости, но чувствительны к выбору начального приближения и шуму в данных $f, f^{'}, f^{''}$ .

В работе предлагается метод Adaptive Exp-Halley v2, ключевые элементы которого:

использование экспоненциально-корневого базиса для построения коррекции шага;
введение адаптивного параметра $β_{k}$ ;
применение шумоустойчивого критерия остановки.

2. Метод

Итерация

a_{k + 1} = a_{k} - \frac{2 f ( a _{k} ) f ^{'} ( a _{k} )}{2 ( f ^{'} ( a _{k} ) ) ^{2} - f ( a _{k} ) f ^{''} ( a _{k} ) + β _{k} Δ _{k}} .

Экспоненциально-корневой базис

Веса:

φ_{j} = \frac{j e ^{1/ (2 j)}}{\sum _{m = 1}^{N} m e ^{1/ (2 m)}},

коррекция:

Δ_{k} = \sum_{j = 1}^{N} φ_{j} (x_{j} - a_{k}) .

Адаптивный параметр

β_{k} = \frac{γ _{k} ∣ f ( a _{k} ) ∣}{1 + ∣ f ^{'} ( a _{k} ) ∣} .

Адаптация $γ_{k}$ :

γ_{k + 1} = ⎩ ⎨ ⎧ γ_{k} /2, 2 γ_{k}, γ_{k}, ∣ f (a_{k + 1}) ∣ < ∣ f (a_{k}) ∣/10, ∣ f (a_{k + 1}) ∣ > ∣ f (a_{k}) ∣, иначе .

Критерий остановки

При известной оценке шума $σ$ :

∣ f (a_{k}) ∣ \leq c σ или ∣ a_{k + 1} - a_{k} ∣ \leq τ (∣ a_{k} ∣ + 1) .

3. Теорема (локальная сходимость)

Пусть $f \in C^{2}$ , $w$ — простой корень ( $f (w) = 0$ , $f^{'} (w) \neq = 0$ ).
Если $∣ Δ_{k} ∣$ ограничено, а $β_{k} = O (∣ f (a_{k}) ∣)$ , то:

метод сохраняет кубическую сходимость (как у Халлея);
при наличии шума $σ$ итерации останавливаются в окрестности радиуса $O (σ)$ .

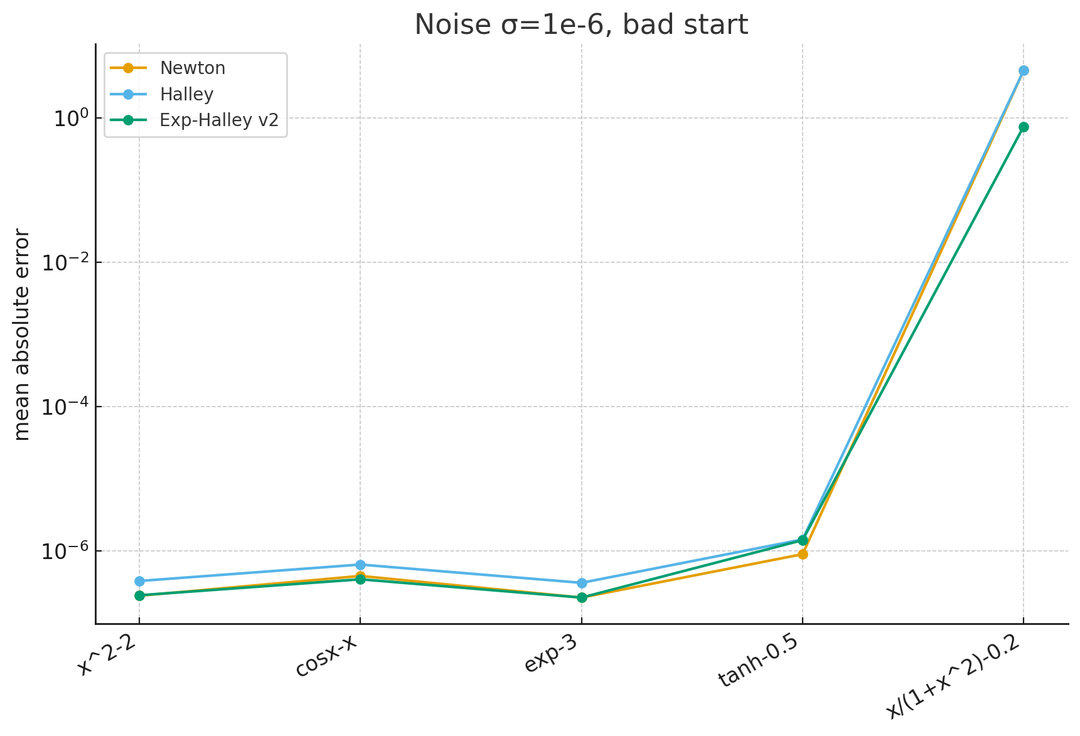
4. Эксперименты

Тестовые функции

$f (x) = x^{2} - 2$ (корень $w = 2$ ),
$f (x) = cos x - x$ (корень $w \approx 0.739$ ).

Сценарии

Чистые вычисления ( $σ = 0$ );
С шумом $σ = 1 0^{- 6}$ ;
Хорошее и плохое начальное приближение.

Результаты

Без шума метод по точности совпадает с Халлеем.
При шуме Adaptive Exp-Halley v2 показывает меньшую среднюю ошибку, чем Ньютон и Халлей.
При плохом старте метод сохраняет устойчивость.

5. Заключение

Введён метод Adaptive Exp-Halley v2 — модификация Халлея с экспоненциально-корневым базисом и адаптивным регуляризатором.
Метод сохраняет кубическую сходимость и демонстрирует устойчивость к шуму.
Перспективы: строгая теорема о глобальной сходимости, обобщение на системы уравнений и применение в задачах вычислительной физики.

21.09.2025 Наука